The Eye Beguiled
6. Origins and history


During the search for impossible objects existing prior to 1934, the year in which Oscar Reutersvärd began to concern himself consciously with the subject, it emerged that such objects were chiefly to be found in art of the age before the advent of classical perspective. They were created unconsciously, but always for a specific purpose.
The oldest example known today is found amongst some miniatures from the Pericope of Henry II, compiled before 1025 and now preserved in the Bayerische Staatsbibliothek in Munich. The Madonna and Child shown above left, taken from an Adoration of the Magi, contains a central pillar which ought to end in the foreground. If it did, however, it would obscure our view of the enthroned virgin. Instead, the top half of the pillar appears in the front pictorial plane, but the bottom half is depicted in the rear, creating an impossible object of the "multiple plane" category.
Another important example is found in the 15th-century fresco of an Annunciation in the Grote Kerk in Breda (above right). Art historian J. Kalf was the first to note something odd about the central pillar. This impossible object seems closely related to the Pericope miniature, both in terms of its character and the reason for its invention.
The conscious construction of an impossible object is a relatively new phenomenon. In 1934 Oscar Reutersvärd drew the first impossible tri-bar. Escher invented the impossible cube in 1958 and incorporated it into his lithograph, Belvedere. The article by Penrose and his son on the impossible tri-bar structure and the continuous flight of steps appeared that same year; Escher took these two figures as the models for his Waterfall (1961) and Ascending and descending (1960). We have a relatively clear overview of these more recent developments thanks to information received by the author at first hand.
We shall be seeing in the second part of this chapter, however, that impossible objects, whether created consciously or unconsciously, have existed in art for a considerably longer period. Indeed, the earliest known examples date from as far back as the 11th century.
Oscar Reutersvärd: the Nestor of impossible objects
Remarkably, Reutersvärd drew his first impossible object quite by chance. Nevertheless, he quickly realized that the figure possessed special, previously undrawn properties. He takes up the story in the following excerpts from his own letters on the subject: "At senior school I had Latin and philosophy instead of maths and biology. In our Latin lessons, while the teacher was offering edifying observations on the Romans, virtually every pupil would be doodling in the blank margins of his Latin grammar. I used to try drawing stars with four, five, six, seven or eight points that were as regular as possible. As I was elaborating a six-pointed star with a circle of cubes one day, I discovered that the cubes had formed a strange constellation. Driven by an inexplicable impulse, I added another three cubes to the configuration, in order to make a triangle. I was sharp enough to realise that I had thereby drawn a paradoxical figure. After the class I showed it to one of my schoolmates, Jan Cornell, because he was my friend and was mad on maths. "I've never seen anything like that before!", he cried. "You must look it up in a mathematical encyclopaedia right away; you're bound to find something on such extraordinary geometric objects!" I hurried to the Stockholm municipal library, where I sought in vain for examples of objects with the same remarkable characteristics.
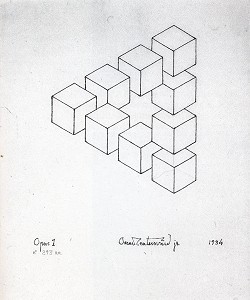
Figure 1. Oscar Reutersvard, "Opus 1 n° 293 aa", 1934
Over the next few years I occasionally played with the possibilities of 'cubes in paradoxical combinations', creating the endless staircase and figures of the devil's fork type. My devil's fork was slightly different, by the way, to the figure subsequently published by Schuster; mine was derived from impossible meanders (fig. 29). At the time I called my figures 'illusory bodies'.
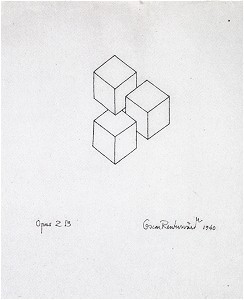
Figure 2. Oscar Reutersvard, "Opus 2B", 1940
In 1958 the same Jan Cornell (now a well-known publisher) gave me an article to read in which the two Penroses introduced a number of impossible objects; it was only then that I realized what I had actually discovered as a boy. Up to that point I had drawn about a hundred impossible objects, but the Penrose article inspired me to begin a thorough exploration of the field. I have drawn a total of approx. 2500 impossible objects between then and now [1986]."
Reutersvärd's account of how he arrived at the endless staircase also sheds light on the way in which his impossible objects arose in the form of related series: "A few days before making the journey from Stockholm to Paris (May 1950), I heard on the radio an interesting programme on Mozart's method of composition. His manner of working was described as 'creative automatism'. Each musical inspiration that he wrote down itself inspired a new idea, and this another, and so on. I felt this was an apt description of the way in which I myself developed impossible objects. I decided to note the time and place of origin on a sequence of impossible objects which I drew during my journey in this 'unconscious', automatic way. It was an arduous experiment, but one that was both interesting and fruitful, and which enabled me to trace the development of increasingly complex figures step by step. I produced fourteen drawings during the almost 40-hour trip. Strangely enough, I did not realise at the time that the figure was in fact a continuous flight of steps. I only consciously began to address the subject some years later" (figs. 3-5).
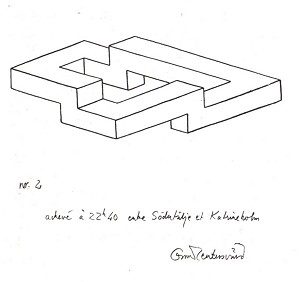
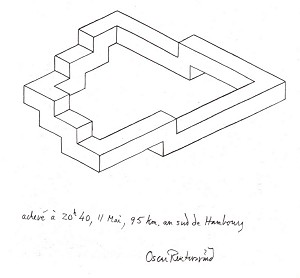
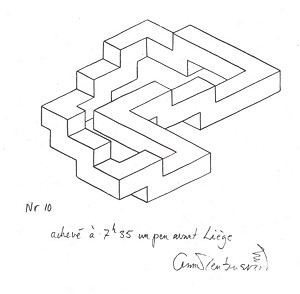
Figure 3-5. Oscar Reutersvärd, travelling sketches, 1950
Writing about Escher, Reutersvärd acknowledged: "I am a very, very great admirer of Escher. I saw one of his impossible objects for the first time in 1961, when Jan Cornell sent me his Ascending and descending. I was very impressed by it, although not so much by the irregularity of the stairs (2x15 + 2x9).
In 1962 Cornell sent me a reproduction of Escher's Waterfall, a remarkable composition in which I particularly admired Escher's treatment of the tri-bar theme. In 1963 and 1964 I wrote Escher two letters, in which I expressed my admiration for his work. He did not reply. I sent him extracts from articles on his work appearing in Swedish newspapers, but again he failed to respond."

Figure 6. Stockholm 1934: Oscar Reutersvärd (right) and Jan Cornell (second from left)

Figure 7. Oscar Reutersvärd, 1950
Drawing something truly impossible
At the Escher Congress in March 1985 in Rome, I talked to Roger Penrose about the role which he and his father had played in rediscovering the impossible tri-bar structure and the continuous steps. He seems to have been greatly inspired by Escher's work, although at that time Escher had not yet drawn any impossible objects, and indeed had no idea even of their existence. Penrose tried drawing a truly impossible object for himself. As he explains: "My own interest in impossible objects stems from the year 1954, when, as a research student, I attended the International Congress of Mathematicians in Amsterdam. I knew one of the speakers, and he remarked that I might be interested in an exhibition of works by the Dutch graphic artist M.C. Escher, an exhibition which had deliberately been organized to run parallel to the congress. I went to see it, and I remember that I was absolutely spellbound by his work, which I was seeing for the first time.

Figure 8. Roger Penrose, Rome, 1985 (photo: Bruno Ernst)
On my journey back to England, I determined to make something 'impossible' myself. I experimented with various designs of bars lying behind and in front of each other in different combinations, and finally arrived at the impossible triangle (later known as the impossible tri-bar) which, it seemed to me, represented the impossibility which I sought in its purest form.
Although Escher had many extraordinary things on display in his exhibition, there was nothing which we would today call an impossible object. I showed my father the above-mentioned triangle at the next possible opportunity. He immediately sketched a number of variants and eventually came up with the drawing of an impossible flight of stairs leading continually downwards (or upwards). We wanted to publish our findings, but had no idea how or where, since we didn't know what field our subject fell into. It then occurred to my father that he knew the editor of the British Journal of Psychology and could ask him whether he would print our article. We decided, therefore, that it was a psychological subject, and sent him our short manuscript. It was published in 1958. We acknowledged the catalogue of the Escher exhibition which I had seen in Amsterdam. When the copies appeared, we sent one to Escher as a token o f our esteem. At that time none of us knew of the much earlier work by Oscar Reutersvard, which I only discovered in 1984."
The much discussed article by the two Penroses is reproduced in full below.
"Impossible Objects: A Special Type of Visual Illusion"
By L.S. and R. Penrose, University College, London, and Bedford College, London. (Manuscript received 30 November 1956)
"Two-dimensional drawings can be made to convey the impression of three-dimensional objects. In certain circumstances this fact can be used to induce contradictory perceptual interpretations. Numerous ideas in this field have been exploited by Escher (1954). The present note deals with one special type of figure. Each individual part is acceptable as a representation of an object normally situated in three-dimensional space; and yet, owing to false connexions of the parts, acceptance of the whole figure on this basis leads to the illusory effect of an impossible structure. An elementary example is shown in Fig.[9]. Here is a perspective drawing, each part of which is accepted as representing a three-dimensional rectangular structure. The lines in the drawing are, however, connected in such a manner as to produce an impossibility. As the eye pursues the lines of the figure, sudden changes in the interpretation of distance of the object from the observer are necessary. A more complicated structure, not drawn in perspective, is shown in Fig.[10]. As this object is examined by following its surfaces, reappraisal has to be made very frequently.
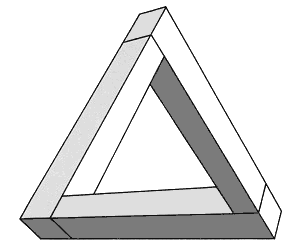
Figure 9.
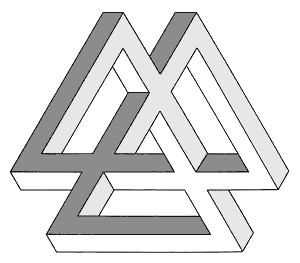
Figure 10.
Another way of presenting the same type of illusion is to express the impossibility in terms of such a phenomenon as a continually descending or ascending path. The flight of steps drawn in Fig.[11] is an example of this. Each part of the structure is acceptable as representing a flight of steps but the connexions are such that the picture, as a whole, is inconsistent: the steps continually descend in a clockwise direction.
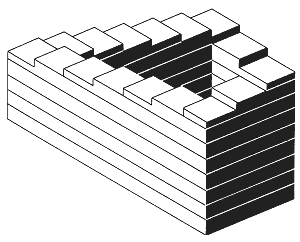
Figure 11.
Actual objects suitably designed, viewed from particular angles, can give exactly the same impressions as inconsistent drawings. A photograph of a model of this kind, apparently an impossible staircase, is shown as Fig.[12]. Actually the far right hand step was much nearer to the camera and much higher than the step which appears to be just above it. Illusions with a different purpose, constructed in a somewhat similar manner, have been discussed by Kilpatrick (1952)."

Figure 12.
References:
Escher, M.C. (1954): Catalogus 118; Stedelijk Museum, Amsterdam.
Kilpatrick, F.P. (1952): "Elementary demonstrations of perceptual phenomena". In Human Behavior from the Transactional Point of View. Hanover, N.H.: Institute for Associated Research.
Escher's impossible cube
When Escher started working on his lithograph Concave and convex in 1955, he was already thoroughly acquainted with the ambiguity of the Necker cube; he was looking for a means of combining the constantly alternating orientations of the cube into an object which allowed two mutually exclusive interpretations at once, and was thus impossible. He succeeded most happily in 1957, with his Cube with magic bands (fig. 16). The preliminary studies for this picture show that Escher was already relatively adept at handling impossible tri-bars.

Figure 13. M.C. Escher, 1985 (photo: Bruno Ernst)
One year later, Escher invented an impossible cube in which the Necker cube is no longer ambiguous but has become a "stable" impossible object. He thereby drew upon the discoveries which he had made in the field of impossible connections of bars. His first sketches on the theme do not yet employ impossible overlapping, but in the final form, which he used for the picture Belvedere, such overlapping is present. The ingenious structure of this impressive picture (known as the "Phantom House" in its early stages) deserves closer examination.
In Chapter 5 we met the principle according to which large numbers of impossible cuboids can be constructed. The majority - including the version which Escher chose for his Belvedere - are positively taxing on the viewer. The EYE tries to make something of them, but its efforts are thwarted by the blatant contradictions built into their geometrical details. Only through the harmonious interplay of such impossible elements with additional perspective information can the picture as a whole reveal the beauty of the impossible cube - and hence the reality and magnificence of the impossible!
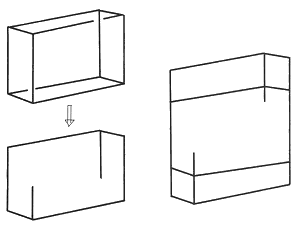
Figure 14. Analysis of the structure of Escher's "Belvedere" (cf. fig. 18), lithograph, 42.2 x 29.5 cm, 1958
Escher was a master of this art. Examining his Belvedere (fig. 18) more closely, we are struck by the very unobtrusiveness of the impossible cuboid at the centre of the composition; its horizontal planes are long and narrow, while those of its parts having contradictory spatial orientations lie far apart and are even camouflaged. This is not at all the solution we might expect, since it seems to obscure the very elements which make the object impossible. Escher takes a further step in this direction by concealing the ceiling behind arcades and the floor behind a balustrade. What remains of the impossible cuboid is shown in Figure 14. Above and below its skeletal framework Escher now builds solid, detailed blocks, with which he both reinforces the reality of the picture as a whole and at the same time accentuates the conflicting orientations of the top and bottom of the cuboid. Thus the upper storey appears to lie at right angles to the one below - an impression heightened by the different directions in which the woman on the top floor and the man on the floor below are each gazing. A minimum of four pillars are necessary to connect the top and bottom planes of an impossible cube, whereby only two can be "impossible"; here, Escher uses eight pillars, six of them establishing impossible connections. The ladder leading from the floor to the ceiling represents another such connection, and one whose impossibility is underlined by the two figures climbing its rungs: the lower figure sets off from inside the cuboid, while the upper figure has somehow arrived outside. Escher uses all these manipulations to infuse his picture with a greater degree of impossibility than that initially achieved by concealing contradictory elements. It is clear that he developed the composition with great care, in order to portray the wondrous nature of the impossible cuboid as realistically as possible.
Figure 15. M.C. Escher, preliminary study for "Cube with magic bands"
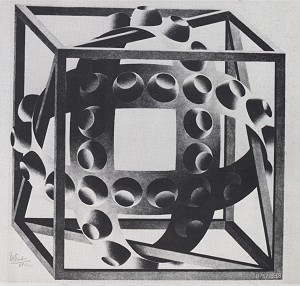
Figure 16. M.C. Escher, "Cube with magic bands", lithograph, 30.9 x 30.9 cm, 1957
Figure 17. Sandro del Prete, pencil drawing, 36.5 x 25.2 cm, 1985. Escher's "Belvedere" may be seen as a coherent construction in which a number of connections are curved.

Figure 18. M.C. Escher, "Belvedere", lithograph, 46.2 x 29.5 cm, 1958
Escher and Penrose
In a letter to his son Arthur of 24 January 1960, Escher described how the Penrose article first came to his notice. At the time, he was "working on the design of a new picture, which featured a flight of stairs which only ever ascended or descended, depending on how you saw it. Seen in the round, a winding staircase would normally take the shape of a spiral, vanishing into the clouds at the top and into hell at the bottom. Not so with my stairs: they form a closed, circular construction, rather like a snake biting its own tail. And yet they can be drawn in correct perspective: each step higher (or lower) than the previous one. A number of human figures are following the stairs in two directions. Those on one side toil ever upwards, while those on the other are trapped in a never-ending descent. I discovered the principle in an article which was sent to me, and in which I myself was named as the maker of various 'impossible objects'. But I was not familiar with the continuous steps of which the author had included a clear, if perfunctory, sketch, although I was employing some of his other examples."

Figure 19 (above) and Figure 20 The underlying structure of Escher's "Ascending and descending" can be interpreted in two ways. Escher himself explained it in terms of Fig. 19, which cannot be described as an impossible object. I adopted the same explanation in my book, "The Magic Mirror of M.C. Escher".
Escher's work provides no explicit evidence that he knew of the impossible tri-bar prior to reading the Penrose article. Nevertheless, the sketches for Cube with magic bands demonstrate that he was indeed preoccupied with similar concerns. But it was the endless stairs which captivated Escher above all else, despite the "perfunctory drawing". He subsequently (18 April 1960) wrote to the two Penroses: "A few months ago, a friend of mine sent me a photocopy of your article ... Your Figures 3 and 4, the 'continuous flight of steps', were entirely new to me, and I was so taken by the idea that they recently inspired me to produce a new picture, which I would like to send you as a token of my esteem. Should you have published other articles on impossible objects or related topics, or should you know of any such articles, I would be most grateful if you could send me further details." Penrose responded with a letter of thanks and an article on a new type of impossible object. The picture which Escher had sent was Ascending and descending (fig. 21), the least original of Escher's four pictures of impossible objects and no more than a "clothed" version of the Penrose drawing. Escher himself never understood how its impossibility actually arose. In The Magic Mirror of M.C. Escher, I offered an analysis of the picture on the basis of Escher's own explanations. Only years later did I realize that Ascending and descending as Escher interpreted it was not an impossible object, but rather a distorted figure which could very probably be built in three dimensions, whereas the Penrose stairs are truly impossible.

Figure 21. M.C. Escher, "Ascending and descending", lithograph, 32.5 x 28.5 cm, 1960
Escher houses his stairs on top of a building. As he understood it, it would be possible to wind strips of tape in a spiral around the exterior of this building. By means of a slight angling, uniformly distributed across every corner and plane, it would then be possible to create the illusion of a continuous flight of steps, as illustrated in Figure 19. At no point is there any gap in the staircase. In Figure 20, on the other hand, all four sides lie horizontal. The hatched strip should end at A, but by adding length B we create an (impossible) connection with strip C: this is the impossible object which is discussed in the Penrose article and which, executed as a model, produces a staircase with a gap in it. It is naturally impossible to tell from Ascending and descending which of the two methods it employs; what is clear, however, is that the difference between the possible and the impossible is very small in such a richly-detailed composition. Escher made true use of Penrose's tri-bar in his Waterfall lithograph of 1961 (fig. 22). Through a series of sketches, any one of which could have produced an attractive impossible object, he arrived at a tri-bar in a thoroughly natural-looking setting with highly realistic details. Geometric impossibility is here accentuated by physical impossibility. Escher organizes the whole into a perpetuum mobile of the first order: the water in his picture is made to drive a water wheel which is thus able to generate power from nothing!

Figure 22. M.C. Escher, "Waterfall", lithograph, 38 x 30 cm, 1961
Waterfall was the last of the four impossible pictures which Escher completed. Having, in his opinion, now successfully depicted the peculiar nature of impossible objects, he returned to the subject to which he was irresistibly drawn and which he considered his personal speciality: the regular filling of planes. Escher was the first to draw an impossible cube; he also knew how to visualize a number of other impossible objects in highly plastic, indeed almost narrative form. Perhaps his chief significance for impossible objects lies in the fact that, through his pictures, they have won greater popularity and international recognition as an enrichment to our visual world.

Figure 23. M.C. Escher, sketches of impossible objects

Figure 24. Mathieu Hamaekers, "Escher's Waterfall, rotated through 45° and conceived as a coherent construction", pencil drawing, 29 x 29 cm, 1985
The devil's fork
Impossible objects with ambiguous contours, characterized by the fact that they cannot be coloured in (cf. fig. 25), were being created by Oscar Reutersvärd even before 1958. It was not until 1964, however, that attention was drawn to such objects in a short article by D.H. Schuster, dedicated to impossible objects of a type that soon became known as the "devil's fork" (article on page 81).
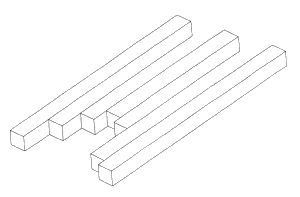
Figure 25. Oscar Reutersvärd, tri-seven-bar structure
A new ambiguous figure: a chain joint/a horizontal brace
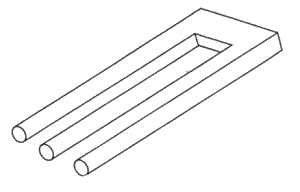
Figure 26.
"The figure opposite (Fig. 26), which recently appeared in an Aviation Week and Space Technology (80, 1964) advertisement, is shown here because, in my opinion, it is a matter of a new type of ambiguous figure. Unlike other ambiguous drawings and geometric figures Jastrow's duck-rabbit, Hill's wife-and-mother-in-law, Botwinick's husband-and-father-in-law (a male counterpart to Hill'' drawing), the Necker cube, the Schroder stairs and Mach' book - it is the shift in the optical focal point which plays a role in perception and interpretation here. If the observer focuses on the left-hand side of the figure at reading distance, he sees three legs, and the right-hand side remains blurred and fuzzy; if he focuses on the right-hand side, he sees a U-shaped object, like a chain joint/horizontal brace. Only if he looks at the middle or slowly allows his view to pass over the figure does he come to realize that he is looking at an 'impossible object', as impossible as the illusory figures described by Penrose and Penrose and authors referring to them."
Figure 27.
Drawings soon appeared of technically realistic variations upon the "devil's fork" theme (figs. 27 and 28). Reutersvard's thorough understanding of such objects led him to draw more complex structures, such as Figure 25, with three bars made to look like seven, and Figure 29, whose true nature as a "devil's fork" is less easily recognizable.
Figure 28.
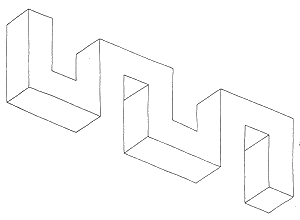
Figure 29. This meander figure has the same properties as the later devil's fork.
Going back in time
Although the history of impossible objects may confidently be said to have started in 1934, some had already appeared before this date. Some were intended as a passing joke, as in the case of Marcel Duchamp; others arose semi-consciously or unconsciously in a desperate attempt to reproduce stereographic elements in a satisfactory manner. These latter were formerly taken as perspective imperfections; today, however, we can appreciate them from an entirely new angle.
In 1916/17 Marcel Duchamp turned an advertisement for Sapolin, a well-known paint manufacturer, into a homage to his friend Apollinaire by omitting and adding various letters (fig. 30). He also transformed part of the bed frame, by means of a few strokes of white paint, into a - not entirely convincing impossible tri-bar and four-bar structure. Duchamp himself never pursued this line any further. To find another example, we must travel back 150 years in time.

Figure 30. Marcel Duchamp, "Apolinere enameled"; corrected ready-made, 1916-17, Philadelphia Museum of Art
Piranesi's fourteenth prison
Giovanni Battista Piranesi (1720-78) was born in Venice. Although destined by his background and training for the architectural profession, in practice he was considerably more active as an etcher and engraver. He published over thirty books on architecture, chiefly polemic works, illustrated with hundreds of drawings of architecture in the neoclassical style. His vast oeuvre commands little interest today. One exception, however, is his series of Carceri - bizarre, fantastical and mysterious drawings of prison dungeons. Invenzioni capricci di carceri, a set of fourteen plates, first appeared in 1745 as the third part of his extensive publications. He subsequently revised all the plates, added two more and republished them in 1760 under the title Carceri d'invenzione (Imaginary Prisons).
Although fantastical depictions of prisons were not uncommon in those days, Piranesi's pictures stand out for the personal, original and powerful nature of their expression. They show increasingly unreal, often impossible rooms in a style which goes beyond neoclassicism.
In Carceri XIV, Piranesi employed the contrast of multiple flat planes as one of the many means with which he consciously sought to create unusual, impossible spaces, without realising, however, that he had thereby achieved an entirely new manner of spatial contradiction.

Figure 31. Giovanni Battista Piranesi, "Carceri, Plate XIV", revised edition, 1760
A great deal has been written about his engravings and several authors have discussed the perspective impossibilities they contain. Some have even seen them as an application of non-Euclidean geometry, and Prof. J.H. van den Berg made them the basis of an important part of his "Metabletica of Matter." These pictures have little to do with non-Euclidean geometry, however. Although consciously striving after spaces which were difficult, if not impossible, to analyse, Piranesi was nevertheless dependent upon contemporary conventions of suggesting three-dimensional space on a two-dimensional surface. He achieved his goal by deliberately including unclear and even contradictory spatial details. He thereby entered the territory of impossible objects, of which a number of examples can be identified in his Carceri. The most obvious is found in the above-mentioned fourteenth engraving, reproduced here in the revised version of 1760 (fig. 31). A long wall featuring three pointed arches starts from the left and runs across and beyond the centre of the picture. At point B (cf. fig. 32) a section of this wall moves forward, whereby the lower half of the wall projects much further into the foreground than the section above. A multiple plane is thus created. Piranesi reinforces this effect by adding a flight of steps (C), which runs parallel to the wall and yet disappears behind it. I have illustrated these main features as accurately as possible, albeit diagrammatically, in Figure 32, through which the impossible object becomes instantly and clearly recognizable.
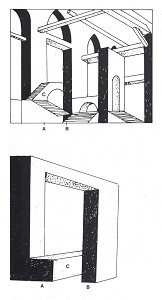
Figure 32. Analysis of Piranesi's "Carceri, Plate XIV"
Hogarth's "false" perspective
Another picture which arose at about the same time, although very different in nature, is equally significant with respect to impossible objects.
The English painter and engraver William Hogarth (1697-1764) is famed as the leading moralist amongst the English painters of the eighteenth century, a reputation which makes us frequently forget that he also executed a number of excellent paintings in the style of the Italian masters of his day. False perspective, a copper engraving from the year 1754 (fig. 33), would surely make him the "father of impossible objects", were it not for the fact that the very purpose of the composition was to demonstrate the types of mistake made by incompetent draughtsmen. As he makes clear in his caption: "Whoever makes a DESIGN without the Knowledge of PERSPECTIVE will be liable to such Absurdities as are shown in this Frontispiece." Here, too, his moralizing tendencies - albeit not aimed, in this case, at the most popular sins of the day come clearly to the fore.

Figure 33. William Hogarth, "False Perspective", engraving, 1754
The angler in the right-hand foreground is standing on a tiled ground whose incorrect vanishing-point makes it look like a vertical wall; this has nothing to do with impossible objects. Behind the angler, the boards of the shed wall compose a flat plane which combines two orientations at once (cf. Chapter 5). A sign hangs overhead from a braced pole, but the spatial configuration this suggests is contradicted by the fact that the pole and the brace are attached to two clearly separate buildings. The sign itself is partially obscured by trees which other spatial pointers place much further away. A woman leaning out of the window in the top right-hand corner is lighting a tramp's pipe with her candle. And yet the tramp is standing on a hill at least a hundred yards from her house...
The other "absurdities" we shall let rest. You will perhaps have noticed that Hogarth at no point uses a precisely definable impossible object. Nevertheless, in composing his loose-knit impossible pictures, he employs the same spatial contradictions that we encounter in self-contained constructions of true impossible objects.
The Mural in Breda
In Breughel's The Magpie on the Gallows (1568; fig. 34), we see a clearly recognizable impossible four-bar. It would not surprise me to learn that the artist had quite consciously depicted something that is entirely out of the ordinary. In trying to make sense of the picture's strange spatiality, we are initially tempted to see the gallows in terms of warped beams. But if we attempt to draw a beam warped in this way, we do not obtain the same result as Breughel. Here, again, we seem to be dealing with a chance but conscious discovery.

Figure 34. Pieter Breughel, detail from "The Magpie on the Gallows", Hessisches Landesmuseum, Darmstadt
It is inevitable that our current preoccupation with impossible objects should make us want to see such objects in historical works, however out of the question this may be. In some cases, nevertheless, the exercise is justified as in the mural in St. Mary's church, or Grote Kerk, in Breda. Here, the testimony of an innocent witness from the period before 1934 lends credibility to the search for impossible objects from the past.
In 1902, a mural measuring 2.7x2.5 metres was discovered beneath the plaster in Breda's Grote Kerk. Remarkably well preserved, it shows an Annunciation from the hand of a fifteenth-century artist (cf. colour reproduction at the beginning of the chapter). The scene is framed by two arches, supported by three pillars. The two outer pillars lie in the foreground, whereas the central pillar ends behind a table towards the back of the room. The result is a flat wall residing in both the front and rear pictorial planes. The first art historian to write about the painting took note of this curious feature, describing it as "a perspectively-misplaced red pillar". However, the artist knew precisely why he was committing this supposed error: he clearly did not wish the scene to be cut in two by the pillar. (We know of other, similarly organized Annunciations, incidentally, in which the central pillar ends in the foreground.)
The colour reproduction indicates the very poor condition of the mural today.
Circumstances favouring unintentional impossible objects
Man first began recording his visual impressions in pictorial form a very long time ago. Of course, all pictorial representations are by definition incomplete and selective, but during that initial (yet nevertheless lengthy) phase, only pictographic elements were reproduced. As objects began to be depicted in greater detail, however, so stereographic elements were added: human figures became three-dimensional, as did their immediate surroundings.

Figure 35. Lorenzo Monaco, detail from the predella of the "Coronation of the Virgin", 1413, Uffizi, Florence
As the striving for a more accurate portrayal of space grew increasingly intense, so artists discovered countless tricks and ploys with which to present a synopsis of perceived spatialities on a two-dimensional surface. This same progression can be traced in every culture in which representation has developed into "art", and in some cases it has led to the flowering of identical artistic ideals: Greece in the 5th century and Italy around 1425 both arrived at a centralized perspective, for example, while an axonometric perspective was preferred e.g. in Japan. We can expect to find unintentional impossible objects wherever an almost self-contained system of representing space has been established. Such systems enable artists to reproduce spatial relationships with a high degree of accuracy; where they fail, this sometimes emerges in the form of spatial contradictions within the picture. Figures 35 and 36 show two works, one by Lorenzo Monaco and the other by Pietro Lorenzetti, dating from the period prior to the invention of centralized perspective. Both artists have managed to establish a spatially coherent floor, but neither has succeeded in incorporating the ceiling without ambiguity. In both cases, what is clearly an interior rear wall in the lower half of the picture appears at the top both to lie much further away and to project forward - almost as if it were an exterior wall. The human figures thereby seem to sit both inside and outside the building at once. An even older painting from Ochrid (fig. 37) conceals a spatial contradiction in its portrayal of Mary's throne. The baldachin at the top is spatially coherent and is correctly related to the foot of the throne by the pillar on the left. This is not the case with the right-hand pillar: the artist has clearly shied away from overlapping the figure of Mary, and a spatial contradiction has arisen. The oldest impossible object currently known to us is a miniature from the 11th century (cf. at the beginning of the chapter).

Figure 36. Pietro Lorenzetti, altarpiece, first half of the 14th century, Uffizi, Florence

Figure 37. Annunciation, Byzantine icon, early 14th century, National Museum, Ochrid
Impossible objects as a sign of cultural change
Centralized perspective, together with the form of perception which accompanies it, represents a binding rule governing the representation of space which we cannot simply abandon without a second thought. We have lived with its maxims for five and a half centuries and judge all representations according to perspective criteria.
Around 1900 a number of new trends began to emerge within the arts. Of the many characteristics distinguishing these movements, one of the most striking was the rejection of traditional spatial representation. One relatively well-defined movement which subsequently emerged, and which became known as Op (or Optical) Art, concerned itself with optical effects and examined the particular way in which our brain processes information. The fact that Op Art is generally dismissed as a passing phenomenon in the history of art reflects first and foremost the selectivity of those writing about art, many of whom have failed to recognize the fact that Op Art is based on the workings of our awareness of living. Op Art has nevertheless become a widely-acknowledged concept within the applied arts and the world of advertising.
While impossible objects demonstrate points of contact with Op Art, it is well possible that they attract interest for more profound reasons. There is no suggestion of any rejection of the laws of spatial representation; on the contrary, impossible objects not only accept and on occasion infringe such laws, but indeed exploit them to create a taut spatiality. The future will show whether the widening interest in impossible objects is indeed more than merely a short-lived artistic experiment. Even today, however, it can be argued that we are concerned here not just with an artistic statement, but rather with a fundamental revision of Western thinking and experience. In 1934 the time was not yet ripe for the work of Oscar Reutersvärd; barely 25 years later, Escher's images captivated broad sections of the public. Escher's style of drawing was comfortably conventional, and thus it was not his manner of expression which attracted such widespread interest, but his sensational subject matter: the exploration of the functioning of our brain. Impossible objects are not the exclusive property of art, however, nor do they belong primarily to the world of mathematical science. Impossible objects can be created amateurishly and inexpertly, and yet still exert a fascination even for those with no head for geometrical formulae. They radiate an aura of self-revelation which directly appeals to a newly-acquired human sensibility. Impossible objects are a sign of this cultural change.
Misunderstandings surrounding impossible objects
Science has many theories which also appeal strongly to a lay public - the "black holes" which have captured the general imagination in our own times are a case in point. Einstein's theory of relativity, the fourth dimension, and non-Euclidean geometry similarly remain very popular. Unfortunately, what remains after the simplifications of third-hand popularization does little justice to the precisely-localized scientific content of the original theory. Some authors have thus been prompted to link the phenomenon of "impossible objects" to scientific concepts shrouded in mystery.
In his - highly recommendable - introduction to Reutersvard's second book, Omöjliga figurer i färg, Carlo Bresti examines in detail attempts to create four-dimensional figures. He thereby arrives at the conclusion that, in this respect, impossible objects represent a breakthrough in art: "As the twentieth century's flight from three-dimensionality has long since taken us down a one-way street to the regions of two-dimensionality, so the art of the next century will flee in the opposite direction, into the realm of the fourth dimension, where continuous steps and triangles with angles totalling 270 degrees will be common accessories."
This has no foundation: even if we incorporate the fourth dimension, a continuous flight of stairs still remains an impossible object, while even in the fourth dimension the angles of a triangle total precisely 180 degrees. The search for a four-dimensional equivalent of an impossible object is nevertheless valid. Indeed, Roger Penrose began looking in 1976, but published nothing on his results. Scott E. Kim (who corresponded with Penrose on the subject) produced an article in 1978 in which he gave a detailed description of an impossible four-dimensional tri-bar, together with instructions on how to reproduce it in three dimensions. Although this "four-dimensional drawing" (drawing in the fourth dimension involves a reproduction in three dimensions!) perhaps means little without the detailed accompanying description of how it arose, we have here reproduced an illustration of a wire model constructed from it (fig. 38). We are also currently waiting for the continually ascending staircase in four dimensions promised in the same article.

Figure 38.
We have already noted that Professor J.H. van den Berg sought to establish parallels between Piranesi's Carceri and non-Euclidean geometry. Reutersvärd does the same when writing about his own impossible objects. Non-Euclidean geometry was similarly one of the topics which arose in the course of my correspondence with the Belgian artist Mathieu Hamaekers. In connection with his superb models of impossible objects, constructed out of curved, twisted bars (cf. Chapter 7), he wrote: "The methods I have developed are based on the geometries of Riemann and Lobachevski. It would be possible to give every culture its own aesthetic, because non-Euclidean modelling offers an infinite number of possibilities. It is important that each culture should be able to express its individuality even in the twenty-first century. This same modelling can also be a compromise between the organic and the mathematical."
While most of us have a vague notion of the fourth dimension, the precepts of non-Euclidean geometry demand closer examination.
Euclid based his geometric system on five axioms (propositions which, although undemonstrated, are accepted as self-evident). Axioms are an indispensable condition of any system of logic, for each proof must be built either upon the preceding proof or upon a proposition (premise) - in this case, Euclid's axioms. Axioms must be used sparingly, in order that something which might have been proved by preceding axioms should not itself be made an axiom.
The fifth Euclidean axiom occupies a special position. It can be formulated as follows: "Through a point P, which does not lie on a given line l, it is possible to draw, in the plane in which both l and P lie, a single line which runs parallel to l."
Up until the first quarter of the last century, leading mathematicians were more or less convinced that the fifth axiom could be proved with the help of the other axioms, although every attempt in this direction failed.
In 1829, Lobachevski showed that dropping the fifth Euclidean axiom resulted in an entirely different geometry. He replaced the fifth axiom by the thesis that no single line can be drawn through a point P outside the line l which is parallel to line l. However much this axiom may appear to contradict our everyday experience, it was nevertheless possible to deduce from it a geometry without inner contradictions. A quarter of a century later, Riemann appeared on the scene with a geometry in which Euclid's fifth axiom was replaced by the postulate that an infinite number of lines can be drawn through P which run parallel to line l. In elaborating these geometries further, we find that their fifth axioms each have different consequences. Thus in Euclid's geometry, the sum of the angles of a triangle is always 180 degrees. In Lobachevski's geometry, the angles of a triangle always total less than 180 degrees, while Riemann's geometry produces triangles whose angles always total more than 180 degrees. We must emphasize, however, that all this has little or nothing to do with impossible objects, nor with their spatial realization in the form of models. For while their geometrical models can be described precisely in Euclidean terms, the impossible objects themselves defy definition even in non-Euclidean geometries. They continue to owe their fascination and "possibility" - their reality, in other words - to the manner in which our visual system functions.
In the field of logic, too, attempts have been made to establish a connection between impossible objects and paradoxes. If we take the term "paradox" in its broadest sense, we can speak without hesitation of logical and visual paradoxes. In this case, impossible objects surely fall into the category of visual paradoxes.
Concentrating upon the structure of a logical (perhaps even linguistic) paradox, however, will certainly not lead to a better understanding of impossible objects. M.J. Cresswell has attempted to define impossible objects using the categories of logic. Although an interesting approach, it casts no new light on their nature. From the literature upon which he draws, moreover, it is clear that he had little opportunity to orientate himself within the fields of the functioning of the visual system and research into impossible objects. In his conclusion, he simply expresses the hope that new light may be shed on the problems from the point of view of logic and semantics, and by none other than ... impossible objects!

Figure 39. Sandro del Prete, "Winding staircase up to Belvedere II", pencil drawing
