The Eye Beguiled

4. Impossible objects

Figure 1.

This is an impossible tri-bar. It is not the illustration of a spatial object, for such an object cannot exist. Yet our EYE accepts both this fact and the object without further ado. We may subsequently come up with a variety of logical arguments - how C, for example, lies in a horizontal plane, while A moves towards us and B away from us, and how, if A and B are constantly moving away from each other, they cannot possibly meet at the top as they apparently do. We might point out that the tri-bar forms a closed triangle, all three sides are perpendicular to each other, and the sum of their internal angles thus totals 270 degrees - which is impossible. As a third line of attack, we might enlist the aid of a principle of stereometry, namely that three non-parallel planes always meet at a single point. In Figure 1, however, we see that:

• dark-grey plane C meets white plane B; the line of intersection is l;
• dark-grey plane C meets light-grey plane A; the line of intersection is m;
• white plane B meets light-grey plane A; the line of intersection is n;
• lines of intersection l, m and n intersect at three different points.

The figure in question thus demonstrably fails to satisfy the stereometric stipulation that three non-parallel planes (here A, B and C) should meet at a single point.

To recap: however simple or complex our subsequent reasoning, the EYE signals such internal contradictions without the slightest explanation.

The impossible tri-bar is paradoxical in several respects. The eye takes no more than a split second to transmit the message: "This is a closed object composed of three bars." This is followed a moment later by: "This object cannot in fact exist..." The third message might read: "... and so the first impression was incorrect." In theory the figure should dissolve into a set of lines bearing no meaningful relationship to each other and no longer organized into the shape of a tri-bar. But this does not happen; instead, the EYE signals afresh: "It is an object, a tri-bar." In short, the conclusion is that it is an object and it is not an object - and herein lies the first paradox. Both interpretations are argued with equal conviction, as if the EYE were leaving the final verdict to some higher authority.

A second paradoxical feature of the impossible tri-bar emerges from the reasoning surrounding its construction. If bar A moves towards us and bar B moves away from us, yet they still meet, the corner that they form must lie in two places at once, one near the viewer and one further away. (The same naturally applies to the other two comers, since the object remains identical in shape even if we turn it so that a different comer is pointing upwards.)

Figure 2. Bruno Ernst, photograph of an impossible tri-bar, 1985
Figure 3. Gerard Traarbach, "Perfect timing", oil on canvas, 100 X 140 cm, 1985, printed in reverse
Figure 4. Dirk Huizer, "Cube", irisated screenprint, 48x48 cm, 1984

The reality of impossible objects

One of the most perplexing questions asked of impossible objects concerns their reality: do they exist or not? The drawing of the tri-bar naturally exists; of that there can be no doubt. At the same time, however, there can also be no doubt that the three-dimensional form presented to us by the EYE does not exist as such in the outside world. For this reason we have chosen to speak of impossible objects rather than impossible figures (as they have more commonly become known in the English language). This would seem a satisfactory means of resolving the dilemma. And yet when we examine, for example, the impossible tri-bar more closely, its spatial reality continues to force itself upon us.

Confronted by the individual parts in disassembled form (fig. 6), it is almost impossible not to believe that simply bolting together the bars and cubes will produce the desired tri-bar.

Figure 3 will have a special appeal for crystallographers. The object appears to be slowly growing; the cubes slot themselves into the existing crystalline grid, and there is no irregularity.

The photograph (fig. 2) is real, although the tri-bar - an arrangement of cigar boxes photographed from a certain angle - is not. It is a visual joke which I devised for Roger Penrose, co-author of the first article on the impossible tri-bar.

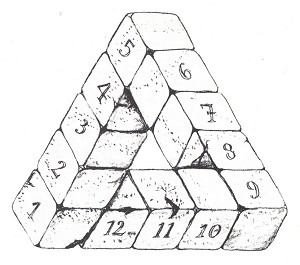
Figure 5.

Figure 5 shows a tri-bar made up of numbered blocks measuring 1xlx1 dm. Simply by counting the blocks, we can work out that the figure has a volume of 12 dm³ and a surface area of 48 dm².

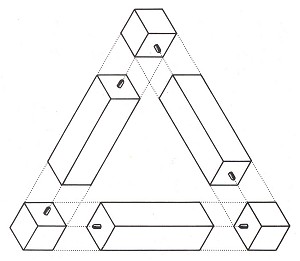
Figure 6.
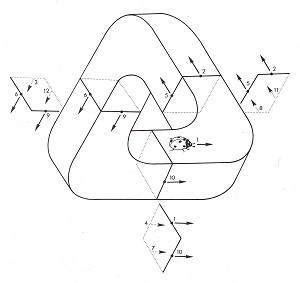
Figure 7.

In a similar way, we can calculate the distance travelled by e.g. a ladybird walking its way round the tri-bar (fig. 7). The mid-point of each bar is numbered and the direction of travel is indicated by arrows. The surface of the tri-bar thereby appears to consist of a long, uninterrupted track; the ladybird must complete four circuits before arriving back at its starting-point.

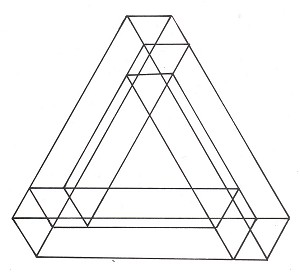
Figure 8.

You might be starting to suspect the impossible tri-bar of harbouring some "secret" on its invisible side. But a transparent view of the impossible tri-bar can be drawn without difficulty (fig. 8). Here, all four neighbouring side planes are visible. The object thereby loses none of its reality.

Let us pose the question once more: what reality does the impossible tri-bar, which can be interpreted and manipulated in so many ways, ultimately have? We should remember that the EYE processes the retinal image of an impossible object just as it would the retinal image of a chair or a house. The result is a "spatial image". In this stage there is no difference between an impossible tri-bar and an ordinary chair. The impossible tri-bar thus exists in the depths of our brain, and indeed at exactly the same level as all the other objects we see surrounding us. The EYE's refusal to affirm its three-dimensional viability in the outside world in no way lessens the fact of the presence of the impossible tri-bar inside our head.

In Chapter 1 we met a type of impossible object whose substance appeared to vanish into nothing. In his pencil drawing of a Passenger train (fig. 11), Fons de Vogelaere subtly works this same type into the reinforced corner pillar at the left of the picture. If we follow the pillar down from top to bottom or cover the lower section of the picture up to the tracks, we see a pillar supported by four buttresses (of which only two are visible). Seen from below, however, the same pillar reveals a relatively wide gap through which the train can pass. Solid blocks of stone are thus simultaneously ... thin air!

This type of object is easy enough to categorize, but proves particularly complex when we come to analyze it. Researchers such as Broydrick Thro have shown that the very description of the phenomenon leads to contradictions. The conflict is one of boundaries. The EYE first calculates contours (outlines) and, from these, shapes which are bounded. Confusion arises when, as in Figure 11, these contours serve a dual purpose.

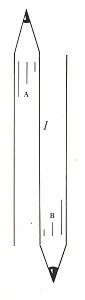
Figure 9.

The same situation arises in Figure 9 (itself an impossible object). In this figure, contour line l manifests itself both as the boundary of volume A and as the boundary of volume B. It is not the boundary of both simultaneously, however. If our eyes fall first upon the upper half of the figure, l is perceived as the boundary of A and remains so until A opens out and is no longer a volume. At this point the EYE offers a second interpretation of l, namely that it is the boundary of B. If we follow the line back up to its start, our new conclusion will in turn be replaced by the first.

If this were its only ambiguity, we might be tempted to speak of a pictographically ambiguous figure. But it is in fact complicated by additional factors, such as the phenomenon of the figure vanishing into the background, and in particular the spatial notion of the figure formed by the EYE. In this connection you might like to take another look at Figures 7, 8 and 9 in Chapter 1. Since these types of figure always manifest themselves as strongly spatial entities, we can provisionally number them as impossible objects and describe them - albeit not explain them - in the following general terms: the EYE calculates from these objects two different three-dimensional forms which are mutually exclusive and yet simultaneously present. Thus, for example, something can be seen in Figure 11 which seems to represent a solid pillar. At second glance, however, it appears as an opening, a spacious gap through which, as shown in the picture, a train

Figure 10. Arthur Stibbe, "In front and behind", acrylic on cardboard, 50x50 cm, 1986
Figure 11. Fons de Vogelaere, “Passenger train”, pencil drawing, 80x98 cm, 1984

The impossible object as paradox

Figure 12. Oscar Reutersvärd, "Perspective japonaise n° 274 dda", coloured ink drawing, 74x54 cm

At the beginning of this chapter we met the impossible object as a three-dimensional paradox, i.e. as an image whose stereographic elements contradict each other. Before examining this paradox in greater depth, we should consider whether there is such a thing as a pictographic paradox. And indeed there is: think of mermaids, of sphinxes, of the fabulous beasts so often depicted in the art of the Middle Ages and early Renaissance. But it is not the EYE which is offended by such pictographic equations as woman + fish = mermaid; rather, it is our knowledge (in this case, of biology), according to which such a combination is unacceptable. Only where spatial data in the retinal image are mutually conflicting is the "automatic" processing carried out by the EYE brought to a halt. The EYE is not prepared for the processing of such strangely structured material, and we witness the result as a new visual experience.

Figure 13a. Harry Turner, from the series "Paradoxical patterns", mixed media, 1973-78
Figure 13b. Harry Turner, "Corner", mixed media, 1978

We can divide the spatial information contained in the retinal image (when looking through one eye only) into two classes, natural and cultural. The first class, which is also found in pictures, contains information over which the human cultural environment exercises no influence. Such truths of "unspoilt nature", if you will, include the following:

• objects of the same size appear smaller, the further away they are. This is the basic principle of the linear perspective which has played a central role in art since Renaissance times;
• an object which partially obscures another object is nearer than that other object;
• where two objects or parts of objects are organically connected, both are equidistant from us;
• objects relatively far away from us will generally appear less distinct and will reveal a blue haze from an aerial perspective;
• the side of an object facing a source of light is brighter than the opposite side, and shadows point away from the source of light.

Figure 14. Zenon Kulpa, "Impossible figures", ink/paper, 30x21 cm, 1980

In a cultural environment, two further factors play an important role in our assessment of space. We humans have created a living environment dominated by right angles. Our architecture, our furniture and many of our utensils are essentially constructed of rectangular cuboids. One might even say that we have compressed our world into a rectangular system of coordinates, into a world of straight lines, level planes and right angles.

Figure 15. Mitsumasa Anno, "A section of a cube"
Figure 16. Mitsumasa Anno, "A slightly difficult interlocking wood puzzle"
Figure 17. Monika Buch, "Cube in blue", acrylic on wood, 80x80 cm, 1976

Our second, cultural class of spatial information is thus rigid and clear:

• a plane is a flat plane and continues as such until other details inform us that its continuity has been interrupted;
• corners at which three planes meet determine three main directions, in which connection certain zig-zag lines can indicate an extension upwards or downwards.

Figure 18. Tamas Farcas, "Crystal", irisated print, 40x29 cm, 1980
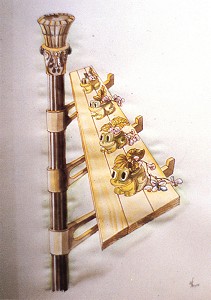
Figure 19. Frans Erens, watercolour, 1985

In our context, the distinction between a natural and a cultural environment is a useful one. Our sense of sight developed in a natural environment, and yet it has the astonishing ability to process, smoothly and accurately, spatial information from the cultural category.

Impossible objects (or at least a large proportion of them) exist thanks to the presence of mutually contradictory spatial statements. In Jos de Mey's Double-guarded gateway to the wintery Arcadia (fig. 20), for example, the flat plane forming the upper section of the wall seems to disperse lower down into several different planes at varying distances from the viewer. This conflicts with the notion of the continuity of the plane. An impression of varying distances is similarly suggested by the overlapping of certain parts of Arthur Stibbe's In front and behind (fig. 10), something again officially prohibited by the rule of the continuity of the flat plane. In a watercolour by Frans Erens (fig. 19), its perspective reduction in size indicates that the plank is running horizontally into the background, yet it is attached to the post in such a way that it must be vertical. In the case of The five bearers by Fons de Vogelaere (fig. 21), we are struck by a number of stereographic paradoxes. Although the drawing is entirely free of paradoxical overlaps, it contains a number of paradoxical connections. The way in which the central figure is joined to the ceiling is particularly interesting. The five load-bearing figures link the ceiling and parapet in so many paradoxical ways that the EYE is sent on a restless search for a point from which best to assess them.

Figure 20. Jos de Mey, "Double-guarded gateway to the wintery Arcadia", acrylic on canvas, 60x70 cm, 1983
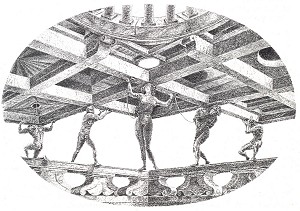
Figure 21. Fons de Vogelaere, "The five bearers", pencil drawing, 80x98 cm, 1985

You may be thinking that, with the aid of every possible type of stereographic element which can occur in a picture, it would be relatively simple to compile a systematic overview of impossible objects:

• those containing perspective elements which are in mutual conflict;
• those in which perspective elements are in conflict with spatial information stated by an overlapping of forms;
• and so on.

We soon realize, however, that we can find no existing examples for many such conflicts, and at the same time that some impossible objects are difficult to fit into such a system. Such categorization might nevertheless enable us to recognize a number of still unknown types of impossible object.

Figure 22. Shigeo Fukuda, "Images of illusion", screenprint, 102x73 cm, 1984

Definitions

Let us conclude this chapter by attempting to give at least a working definition of impossible objects.

In my first publications on Escher's pictures of impossible objects, which appeared around 1960, I arrived at the following formulation: a possible object can always be construed as a projection, a representation of a three-dimensional object. In the case of impossible objects, however, no three-dimensional object exists whose representation is a projection; in this sense we may call an impossible object an illusory representation. This definition is both incomplete and incorrect (a point we shall return to in Chapter 7), because it refers only to the mathematical side of impossible objects.

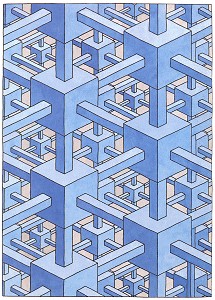
Figure 23. Oscar Reutersvärd, "Cubic organization of space", coloured ink drawing, 29x20.6 cm.
In reality this space is not filled, since the larger cubes are at no point linked to the smaller ones behind.

Zenon Kulpa offers the following definition: the image of an impossible object is a two-dimensional figure which creates the impression of being a three-dimensional object, whereby this figure cannot exist as we spatially interpret it; thus, any attempt to construct it will lead to (spatial) contradictions which are clearly visible to the viewer.

Kulpa's last observation suggests one practical way of judging whether an object is impossible or not: just try building it yourself. You will soon see - perhaps even before you start - if it won't work.

I myself would prefer a definition which emphasizes that the EYE comes away from the impossible object with two contradictory conclusions: it is true and at the same time not true. I would like such a definition to embrace the reason for these mutually conflicting conclusions, and furthermore to make clear the fact that impossibility is not a mathematical property of the figure, but a property of its interpretation by the viewer.

On this basis I propose the following definition:

An impossible object possesses a two-dimensional representation which the EYE interprets as a three-dimensional object, whereby the EYE simultaneously determines that it is impossible for this object to be three-dimensional since the spatial information contained within the figure is self-contradictory.

Figure 24. Oscar Reutersväird, "Impossible four-bar with Crossbars"
Figure 25. Bruno Ernst, "Mixed illusions", photograph, 1985